Η φυσική της μουσικής (με λίγα μαθηματικά) μέρος πρώτο :Χορδές, κλίμακες και κουρδίσματα.

ΠΡΟΕΙΔΟΠΟΙΗΣΗ

Στον πρόλογο του περίφημου «Χρονικού του χρόνου» ο Stephen Hawking  αναφέρει πως κάποιος φίλος του τον προειδοποίησε ότι με κάθε εξίσωση που θα χρησιμοποιούσε θα έχανε και τους μισούς του αναγνώστες. Ο κατά πολύ σοφότερος από εμένα συνάδελφος χρησιμοποίησε μόνο μια. Αν ισχύει κάτι τέτοιο, τότε το παρόν δεν θα διαβαστεί ούτε από τους φίλους μου. Οφείλω λοιπόν να προειδοποιήσω τους επίδοξους αναγνώστες ότι για την πλήρη κατανόηση αυτών που ακολουθούν απαιτούνται Λυκειακά  Μαθηματικά και Φυσική την οποία συνοπτικά και όσο το δυνατόν πιο απλά παραθέτω, με συνοδεία οπτικοακουστικού υλικού.

 

“Σαν μια χορδή που χτυπάει δυνατά μέσα στο στήθος σου
σαν άστρο που σβήνει
και μια μελωδία που πίσω σ’ αφήνει.”

Αλκιβιάδης Κωνσταντόπουλος-Μπάμπης Στόκας : Κι έμεινα εδώ

Αρμονικά μηχανικά κύματα

  Είναι τα πιο απλά κύματα που δημιουργούνται σε κάποιο ελαστικό μέσο διάδοσης, όπως μία χορδή, όταν η πηγή που τα δημιουργεί εκτελεί  απλή αρμονική ταλάντωση . Τα αρμονικά κύματα έχουν την ημιτονοειδή μορφή που φαίνεται στο παρακάτω σχήμα και για τη στοιχειώδη περιγραφή τους χρησιμοποιούμε τρία βασικά φυσικά μεγέθη :

Το μήκος κύματος λ που είναι η ελάχιστη απόσταση ανάμεσα σε δυο τυχαία σημεία του κύματος που έχουν την ίδια κινητική συμπεριφορά. Πρακτικά μήκος κύματος είναι η απόσταση ανάμεσα σε δύο διαδοχικά μέγιστα (όρη) ή δυο διαδοχικά ελάχιστα (κοιλάδες).Το μετράμε σε μέτρα  (m).

Τη συχνότητα f  με την οποία ταλαντώνονται τα σημεία του μέσου διάδοσης και ισούται με το ρυθμό επανάληψης της κυματικής διαταραχής. Την μετράμε σε παλμούς ανά δευτερόλεπτο (χερτζ Hz)

Την ταχύτητα διάδοσης υ  που εξαρτάται μόνο από τις ιδιότητες του μέσου διάδοσης. Αν το μέσο αυτό είναι μια τεντωμένη χορδή τότε η ταχύτητα διάδοσης δίνεται από τη σχέση  :

όπου F είναι η δύναμη που τεντώνει τη χορδή (τάση της χορδής) και μ είναι η γραμμική πυκνότητα μάζας (μάζα ανά μονάδα μήκους) της χορδής. Την ταχύτητα την μετράμε σε μέτρα ανά δευτερόλεπτο (m/s) ενώ τη γραμμική πυκνότητα μάζας σε κιλά ανά μέτρο (kg/m)

Τα τρία φυσικά μεγέθη υ, λ και f συνδέονται με τη θεμελιώδη κυματική εξίσωση:

υ = λ f       (2)

Δημιουργία στάσιμων κυμάτων

Τα στάσιμα κύματα είναι το αποτέλεσμα της συμβολής δύο πανομοιότυπων κυμάτων που διαδίδονται σε αντίθετες κατευθύνσεις, όπως φαίνεται στην προσομοίωση που ακολουθεί. Τα σημεία στα οποία τα κύματα συμβάλλουν αποσβεστικά ή (καταστρεπτικά)παραμένουν ακίνητα και ονομάζονται δεσμοί, ενώ τα σημεία στα οποία τα κύματα συμβάλλουν ενισχυτικά ταλαντώνονται με μέγιστο πλάτος και  ονομάζονται κοιλίες.Η απόσταση ανάμεσα σε δύο διαδοχικούς δεσμούς ισούται με μισό μήκος κύματος (λ/2), ενώ η συχνότητα f της ταλάντωσης των σημείων του στάσιμου κύματος είναι ίση με αυτή των συμβαλλομένων κυμάτων.

 

Δημιουργία στάσιμων κυμάτων σε χορδή που είναι στερεωμένη και στα δύο άκρα.

Στο video που ακολουθεί παρουσιάζεται η συμβολή κυμάτων που προσπίπτουν και ανακλώνται σε ελεύθερο και ακλόνητο άκρο χορδής με αποτέλεσμα τη δημιουργία στάσιμων κυμάτων.

 

Ανάκλαση παλμού και αρμονικού κύματος σε ελεύθερο και σε ακλόνητο άκρο χορδής

 

Ας θεωρήσουμε μια χορδή μήκους L  στερεωμένη και στα δύο της άκρα. Αν την κυρτώσουμε με τέτοιο τρόπο ώστε το παραμορφωμένο σχήμα της να έχει την πρώτη μορφή που φαίνεται στην προσομοίωση που ακολουθεί τότε το στάσιμο κύμα που δημιουργείται έχει δύο δεσμούς (τα άκρα της χορδής) και το μήκος της χορδής ισούται με το μισό του μήκους κύματος (δηλαδή την απόσταση ανάμεσα σε δυο διαδοχικούς δεσμούς)

L = λ₁/2           ή      λ₁= 2 L

Στη δεύτερη μορφή της προσομοίωσης, το στάσιμο κύμα έχει δύο δεσμούς επομένως το μήκος της χορδής ισούται με ένα μήκος κύματος :

λ₂ = L

ενώ στην τρίτη οι τέσσερεις δεσμοί δημιουργούν τρία μισά μήκη κύματος οπότε:

L = 3λ₃/2    ή    λ₃ = 2L/3

Αν η χορδή λοιπόν ταλαντωθεί σχηματίζοντας τις πιο πάνω χαρακτηριστικές μορφές (που ονομάζονται ιδιομορφές) τότε τα μήκη κύματος των στάσιμων κυμάτων που δημιουργούνται σε κάθε περίπτωση είναι καθορισμένα και ικανοποιούν τη σχέση:

όπου ο δείκτης n αντιστοιχεί στη n-οστή ιδιομορφή ταλάντωσης.

Με τη βοήθεια της θεμελιώδους κυματικής εξίσωσης υ = λ f ή f = υ/λ μπορούμε εύκολα να υπολογίσουμε τις συχνότητες (που ονομάζονται ιδιοσυχνότητες) που αντιστοιχούν σε κάθε μια ιδιομορφή, συνδυάζοντάς την με την εξίσωση (3). Έτσι βρίσκουμε ότι οι ιδιοσυχνότητες f_n δίνονται από τη σχέση:

Τέλος αν στην εξίσωση (4) αντικαταστήσουμε την ταχύτητα διάδοσης υ από τη σχέση (1) βρίσκουμε ότι οι ιδιοσυχνότητες f_n υπολογίζονται από τη σχέση:

Η χαμηλότερη ιδιοσυχνότητα αντιστοιχεί στην τιμή  n=1 και ονομάζεται θεμελιώδης (fundamental) συχνότητα f₁. Δίνεται από τη σχέση:

Οι υπόλοιπες ιδιοσυχνότητες ονομάζονται (ανώτερες) αρμονικές και είναι ακέραια πολλαπλάσια της θεμελιώδους. Όλες μαζί οι ιδιοσυχνότητες αποτελούν τη λεγόμενη αρμονική σειρά. Η θεμελιώδης f₁ είναι η πρώτη αρμονική, η ιδιοσυχνότητα f₂ = 2f₁ είναι η δεύτερη αρμονική, η ιδιοσυχνότητα  f_n = n f₁ είναι η n-οστή αρμονική.

(Αν θέλετε να παράγετε κάποιες από τις αρμονικές που βλέπετε στο παρακάτω σχήμα πιέστεεδώ)

Στο video που ακολουθεί μπορείτε να δείτε την παραγωγή των τεσσάρων πρώτων αρμονικών

Παραγωγή των τεσσάρων πρώτων αρμονικών

 

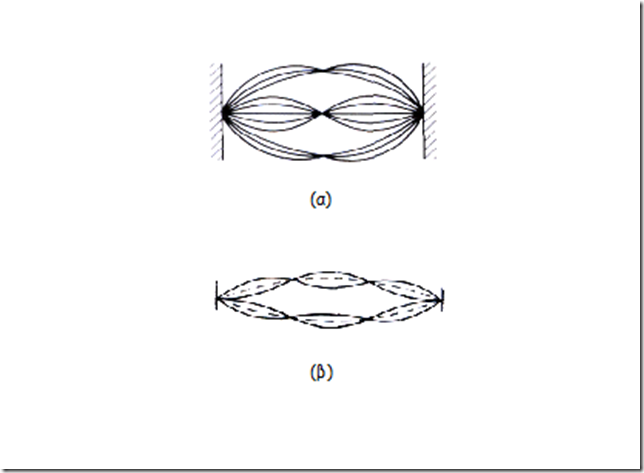
Αν μια χορδή διεγερθεί με τέτοιο τρόπο ώστε το σχήμα της να είναι το ίδιο με εκείνο κάποιας αρμονικής, τότε θα ταλαντωθεί με την ιδιοσυχνότητα της αρμονικής αυτής.Τότε λέμε ότι παράγεται ένας “καθαρός” φθόγγος. Αν όμως απλώς αγγίξουμε με ένα δοξάρι ή με μια πένα ή “τσιμπήσουμε”   μια χορδή τότε αυτή θα ταλαντωθεί σύνθετα και μαζί με τη θεμελιώδη συχνότητα θα εμφανιστούν και πολλές ανώτερες αρμονικές. Έτσι θα παραχθεί ένας “φυσικός” φθόγγος, ο οποίος είναι από φυσική άποψη ένας ήχος.Η χαμηλότερη ιδιοσυχνότητα (θεμελιώδης) καθορίζει τη συχνότητα του φυσικού φθόγγου. Στο σχήμα (α) φαίνεται η δόνηση χορδής η οποία πάλλεται ταυτόχρονα στην πρώτη και δεύτερη αρμονική, ενώ στο  σχήμα (β) η χορδή πάλλεται ταυτόχρονα στην πρώτη και τρίτη.

Όταν έχουμε επαλληλία πολλών αρμονικών τότε τα ηχητικά κύματα που που δημιουργούνται στον αέρα που περιβάλλει τη χορδή, μεταδίδουν στα αυτιά μας και στον εγκέφαλό μας ένα συνολικό αποτέλεσμα που είναι χαρακτηριστικό του συγκεκριμένου εγχόρδου οργάνου. Η χροιά  του ήχου μιας συγκεκριμένης νότας (θεμελιώδους ιδιοσυχνότητας) που παίζεται με ένα όργανο καθορίζεται από τον αριθμό των ανώτερων αρμονικών που εμφανίζονται καθώς και από τις σχετικές τους εντάσεις. Στο σχήμα που ακολουθεί φαίνονται οι κυματομορφές του πιάνου και του βιολιού για την ίδια θεμελιώδη συχνότητα που παριστάνεται με το ημιτονικό κύμα (sine wave).

Σύμφωνα με τη σχέση (5), μπορούμε να μεταβάλουμε τη συχνότητα που παράγει ένα έγχορδο όργανο μεταβάλλοντας είτε την τάση F είτε το μήκος L της χορδής. Η τάση F μεταβάλλεται όταν ο μουσικός στρίβει το κουρδιστήρι της. Αφού ο μουσικός κουρδίσει το έγχορδό του ο μόνος τρόπος για να μεταβάλει τη συχνότητα είναι να πιέσει με τα δάκτυλά του τη χορδή πάνω στο μπράτσο του οργάνου, μεταβάλλοντας έτσι το μήκος της L. Καθώς ελαττώνεται το μήκος, αυξάνεται η συχνότητα και έτσι ο ήχος ακούγεται οξύτερος, αφού σύμφωνα με τη σχέση (5) οι ιδιοσυχνότητες είναι  αντιστρόφως ανάλογες με το μήκος της χορδής  

Η φυσική  διατονική κλίμακα (just diatonic scale)  ή φυσικό κούρδισμα (harmonic tuning).

Ας πάρουμε τις 16 ιδιοσυχνότητες μιας αρμονικής σειράς με θεμελιώδη ιδιοσυχνότητα f₁:

 ΠΙΝΑΚΑΣ 1

 

Για να δημιουργήσουμε τη φυσική διατονική κλίμακα θα κάνουμε δύο παραδοχές:

1. Το ανθρώπινο αυτί είναι περισσότερο ευαίσθητο σε λόγους συχνοτήτων, παρά σε διαφορές.

2. Όσο πιο απλός είναι ο λόγος των συχνοτήτων τόσο πιο εύηχες (σύμφωνες) είναι οι αποστάσεις τους (διαστήματα) (Θεωρία των αναλογιών του Πυθαγόρα)

Έτσι λοιπόν έχουμε:

Ο πρώτος (θεμελιώδης) και ο δεύτερος αρμονικός έχουν σχέση συχνοτήτων f₂ = 2f₁ και δίνουν λόγο  2:1.Λέμε ότι απέχουν διάστημα  μιας οκτάβας (το οποίο ονομάζεται έτσι γιατί περιέχει οκτώ φθόγγους). Όπως βλέπουμε στον  πίνακα 1 μια συχνότητα f_n έχει απόσταση πολλαπλάσια της οκτάβας από μια άλλη f όταν τις συνδέει η σχέση f_n = 2ⁿ f (n = 1,2,3,..). (Οι συχνότητες αυτές επισημαίνονται στον Πίνακα 1 μα κόκκινο χρώμα). Οι φθόγγοι που συνδέονται με την προηγούμενη σχέση παρόλο που έχουν διαφορετικά τονικά ύψη ο τονικός χαρακτήρας τους παραμένει αισθητά ίδιος. Γι αυτό λέμε ότι έχουν τον μεγαλύτερο βαθμό συγγένειας.

Ο δεύτερος και ο τρίτος αρμονικός δίνουν λόγο συχνοτήτων 3:2.Ο φθόγγος με συχνότητα f_3/2 = 3/2f₁  απέχει από τον πρώτο αρμονικό  f₁  διάστημα μιας πέμπτης. Οι φθόγγοι αυτοί έχουν φυσική συγγένεια δεύτερου βαθμού.

Ο τρίτος και ο τέταρτος αρμονικός δίνουν λόγο συχνοτήτων 4:3.Ο φθόγγος με συχνότητα f_4/3 = 4/3f₁  απέχει από τον πρώτο αρμονικό  διάστημα  μιας τετάρτης. Η οκτάβα, η πέμπτη και η τετάρτη ονομάζονται καθαρά διαστήματα. Θεωρείται ότι οι περισσότεροι άνθρωποι σε οποιοδήποτε πολιτισμό ή περίοδο της ιστορίας έχουν κρίνει ότι τα διαστήματα αυτά δίνουν ευχάριστους τονικούς συνδυασμούς και έχουν δημιουργήσει μουσικές συνθέσεις γύρω από αυτά.   

Ο όγδοος και ο ένατος αρμονικός δίνουν λόγο συχνοτήτων 9:8 και ορίζουν φθόγγο με συχνότητα f_9/8 = 9/8f₁  και διάστημα από τον πρώτο αρμονικό μιας μεγάλης δευτέρας (μεγάλος τόνος).

Ο τέταρτος και ο πέμπτος αρμονικός δίνουν λόγο συχνοτήτων 5:4 και ορίζουν φθόγγο με συχνότητα f_5/4 = 5/4f₁  και διάστημα από τον πρώτο αρμονικό μιας μεγάλης τρίτης.

Ο τρίτος και ο πέμπτος αρμονικός δίνουν λόγο συχνοτήτων 5:3 και ορίζουν φθόγγο με συχνότητα f_5/3 = 5/3f₁  και διάστημα από τον πρώτο αρμονικό μιας μεγάλης έκτης.

Τέλος ο όγδοος και ο δέκατος πέμπτος αρμονικός δίνουν λόγο συχνοτήτων 15:8 και ορίζουν φθόγγο με συχνότητα f_15/8 = 15/8f₁  και διάστημα από τον πρώτο αρμονικό μιας μεγάλης εβδόμης.

Αν κατατάξουμε τώρα τους φθόγγους κατά αύξουσα σειρά συχνοτήτων, δημιουργούμε μια επτάφθογγη διατονική (δια των τόνων) κλίμακα (ο 1^ος και ο 8^ος φθόγγος έχουν τον ίδιο τονικό χαρακτήρα) :

f₁   f_9/8   f_5/4   f_4/3   f_3/2   f_5/3   f_15/8   f₂

Τα διαστήματα μεταξύ των φθόγγων της κλίμακας που δημιουργήσαμε είναι:

f_9/8 /f₁ = 9/8 Το διάστημα αυτό ονομάζεται μεγάλος τόνος (Τ).

f_5/4 /f_9/8   = 10/9 Το διάστημα αυτό ονομάζεται μικρός τόνος (τ).

f_4/3 / f_5/4 = 16/15 Το διάστημα αυτό ονομάζεται ημιτόνιο (η).

f_3/2 / f_4/3= 9/8 Μεγάλος τόνος (Τ).

f_5/3/f_3/2= 10/9 Μικρός τόνος (τ).

f_15/8/f_5/3= 9/8 Μεγάλος τόνος (Τ).

f₂/f_15/8= 16/15 Ημιτόνιο (η).

H φυσική κλίμακα λοιπόν προκύπτει με επιλογή συγκεκριμένων απλών λόγων των ιδιοσυχνοτήτων της αρμονικής ακολουθίας. Όλοι αυτοί οι λόγοι παράγονται μαθηματικά ξεκινώντας από την οκτάβα, από την οποία προκύπτει η πέμπτη και η τετάρτη : 2/1 = (2/3) ^. (3/4), από την πέμπτη παράγεται η μικρή και η μεγάλη τρίτη : 3/2 = (5/4) ^. (6/5), από την μεγάλη τρίτη παράγεται ο μικρός και ο μεγάλος τόνος : 5/4 = (9/8) ^. (10/9) και τέλος από τον μεγάλο τόνο παράγεται η μεγάλη έκτη και εβδόμη :9/8 = (15/8) ^. (3/5). Η διαμόρφωση της κλίμακας, με τις βαθμίδες της τοποθετημένες κατά αύξουσα σειρά,  παρουσιάζεται στον παρακάτω πίνακα:

ΠΙΝΑΚΑΣ 2

Στην παραπάνω ακολουθία των φθόγγων έχουμε τα σχετικά με τη συχνότητα f₁ τονικά ύψη. Μπορούμε να χρησιμοποιήσουμε τη σχέση (6) :

και να αποδώσουμε σε κάθε συχνότητα μια τιμή .

Ας θεωρήσουμε ότι έχουμε μια χορδή μήκους L = 0,65m και γραμμικής πυκνότητας μ = 20 10^-5kg/m. Αν την τεντώσουμε με μια δύναμη F = 23,56N και την διεγείρουμε, τότε σύμφωνα με τη σχέση  (6) θα παραχθεί μια θεμελιώδης ιδιοσυχνότητα f₁ = 264Hz. Στη συχνότητα αντιστοιχεί ο τόνος του Ντο⁴ (C⁴) (μεσαίο Ντο). Συνεχίζοντας τους υπολογισμούς για τους υπόλοιπους φθόγγους της κλίμακας έχουμε:

f_9/8= (9/8) ^. 264 Ηz = 297 Hz που είναι η τιμή που έχουμε αποδώσει στον τόνο της νότας Ρε⁴ (D⁴ ) στο φυσικό κούρδισμα.

f_5/4= (5/4) ^. 264 Hz = 330 Ηz που είναι η τιμή που έχουμε αποδώσει στον τόνο της νότας Μι⁴ (Ε⁴ ) στο φυσικό κούρδισμα.

f_4/3= (4/3) ^. 264 Hz = 352 Ηz που είναι η τιμή που έχουμε αποδώσει στον τόνο της νότας Φα⁴ (F⁴ ) στο φυσικό κούρδισμα.

f_3/2= (3/2) ^. 264 Hz = 396 Ηz που είναι η τιμή που έχουμε αποδώσει στον τόνο της νότας Σολ⁴ (G⁴ ) στο φυσικό κούρδισμα.

f_5/3= (5/3) ^. 264 Hz = 440 Ηz που είναι η τιμή που έχουμε αποδώσει στη συχνότητα της νότας Λα⁴ (Α⁴ ).

f_15/8= (15/8) ^. 264 Hz = 495 Ηz που είναι η τιμή που έχουμε αποδώσει στον τόνο της νότας Σι⁴ (Β⁴ ) στο φυσικό κούρδισμα.

f₂= 2 ^. 264 Hz = 528 Ηz που είναι η τιμή που έχουμε αποδώσει στον τόνο της νότας Ντο⁵ (C⁵ ) στο φυσικό κούρδισμα.

Έτσι παίρνουμε την μείζονα (majore) κλίμακα του Ντομε βάση τους απλούς λόγους των αρμονικών της θεμελιώδους ιδιοσυχνότητας του Ντο . Ο χαρακτηρισμός της κλίμακας ως μείζονος έχει να κάνει με την ακολουθία των τόνων και των ημιτονίων με τη συγκεκριμένη σειρά : 2 τόνοι 1 ημιτόνιο, 3 τόνοι 1 ημιτόνια (Πίνακας 3):

ΠΙΝΑΚΑΣ 3

Ακούστε την παραπάνω κλίμακα πιέζονταςεδώ

Το Love Scene είναι ένα κομμάτι γραμμένο στη φυσική διατονική κλίμακα από τον Kyle Gann. Για να δείτε την κλίμακα και την παρτιτούρα πιέστε εδώκαι για να το ακούσετε πιέστεεδώ

Στον Πίνακα 4 φαίνονται οι απόλυτες τιμές των συχνοτήτων του Πίνακα 1. ξεκινώντας από την τιμή της θεμελιώδους ιδιοσυχνότητας f₁ = 264 Hz. Έτσι προκύπτουν οι  φθόγγοι της αρμονικής σειράς του Ντο. Να σημειώσουμε ότι η σειρά εμπεριέχει όλα τα διαστήματα, αρχίζοντας από τα απλά στις χαμηλές συχνότητες, έως τα πιο σύνθετα στις ψηλές.

ΠΙΝΑΚΑΣ 4

Η φυσική κλίμακα παρουσιάζει περισσότερο θεωρητικό ενδιαφέρον, γιατί δίνει μια ερμηνεία των φυσικών κανόνων του τονικού συστήματος, παρά πρακτικό. Υπάρχουν κάποια σημαντικά μειονεκτήματα που καθιστούν τη χρήση της δύσκολη. Κατ αρχήν εμφανίζονται  δυο διαφορετικοί τόνοι με λόγους 9/8 = 1,125 και 10/9=1,11 ενώ το διάστημα που δημιουργούν τα δύο ημιτόνια (16/15)^. (16/15) = 1,14 δε συμπίπτει με κανέναν από αυτούς. (Η διαφορά ανάμεσα στον μεγάλο και μικρό τόνο είναι το διάστημα (9/8) : (10/9) = 81/80 που ονομάζεται σύντονο ή διδυμικό κόμμα). Έτσι αν  θελήσουμε να προσθέσουμε πχ ανάμεσα στο Ντο και το Ρε ένα ημιτόνιο υπάρχουν δύο τρόποι. Είτε να αυξήσουμε τη συχνότητα του Ντο κατά 16/15 παίρνοντας έτσι τη συχνότητα 264 ^. (16/15) = 281,6 Hz και έτσι δημιουργούμε την Ντο#, είτε να ελαττώσουμε τη συχνότητα της Ρε κατά 16/15 οπότε παίρνουμε τη συχνότητα 297 : (16/15) =  278,4 Hz που είναι η Ρε . Διαπιστώνουμε λοιπόν ότι στη φυσική κλίμακα οι αλλοιωμένοι κατά μια ύφεση και κατά μια δίεση φθόγγοι δεν συμπίπτουν.

Ένα άλλο θέμα είναι η αλλαγή τονικότητας. Η μείζονα κλίμακα του Ντο δομήθηκε με βάση τους απλούς λόγους των αρμονικών της θεμελιώδους ιδιοσυχνότητας του Ντο η οποία και αποτελεί το τονικό κέντρο της συγκεκριμένης κλίμακας. Τι θα συμβεί αν θελήσουμε να κάνουμε μεταφορά (τρανσπόρτο) σε έναν τόνο πιο πάνω, δηλαδή σε Ρε μείζονα, ενώ το (φυσικό) μας κούρδισμα είναι σε Ντο; Η απάντηση είναι ότι θα ακούσουμε παραφωνίες εκτός κι αν ξανακουρδίσουμε το όργανό μας σε Ρε. Ένας τρόπος για να να καταλάβουμε γιατί συμβαίνει αυτό  είναι να υπολογίσουμε τις συχνότητες των φθόγγων της φυσικής μείζονος κλίμακας του Ρε ξεκινώντας από την θεμελιώδη ιδιοσυχνότητα στα 297Hz και χρησιμοποιώντας τους ίδιους απλούς λόγους των διαστημάτων, με την ίδια σειρά . Έτσι έχουμε :

Θεμελιώδης ιδιοσυχνότητα f₁ = 297 Ηz

f_9/8= (9/8) ^. 297 Ηz = 334,2 Hz 

f_5/4= (5/4) ^. 297 Hz = 371,3 Ηz 

f_4/3= (4/3) ^. 297 Hz = 396 Ηz 

f_3/2= (3/2) ^. 297 Hz = 445,5 Ηz 

f_5/3= (5/3) ^. 297 Hz = 495 Ηz 

f_15/8= (15/8) ^. 297 Hz = 556,9 Ηz 

f₂= 2 ^. 297 Hz = 594 Ηz 

Αν κάνουμε τώρα τη σύγκριση ανάμεσα στις δυο κλίμακες:

ΠΙΝΑΚΑΣ 5

διαπιστώνουμε ότι οι ιδιοσυχνότητες των φθόγγων Μι και Λα είναι διαφορετικές. Ένα μουσικό όργανο λοιπόν που είναι κουρδισμένο σε μια φυσική μείζονα τονικότητα, παίζει τις άλλες τονικότητες “παράφωνα”. Γι αυτό το λόγο δημιουργήθηκε…

…Η ισοσυγκερασμένη κλίμακα 12 τόνων (twelve-tone equal tempered scale)

Ο ισοσυγκερασμός είναι η μαθηματική διαίρεση της οκτάβας σε δώδεκα ίσα διαστήματα (ημιτόνια).Το ισοσυκγερασμένο κούρδισμα έχει επικρατήσει από το 19ο αιώνα. Η μαθηματική λογική της διαίρεσης της οκτάβας σε ίσα διαστήματα είναι η εξής:

Έστω χ ο λόγος δύο διαδοχικών συχνοτήτων. Τότε η σχέση ανάμεσα στη θεμελιώδη ιδιοσυχνότητα f₁ και την ιδιοσυχνότητα του πρώτου αρμονικού 2f₁ είναι: 2f₁ = x¹² f₁ από την οποία προκύπτει ότι

Στο ισοσυγκερασμένο κούρδισμα διατηρείται ως φυσικό διάστημα μόνο η οκτάβα και το απόλυτο τονικό ύψος της Λα⁴ (Λα του διαπασών), που στο δεύτερο Διεθνές Συνέδριο Χορδίσματος (Λονδίνο 1939) καθορίστηκε να έχει την τιμή των 440 Hz. Με αυτό των τρόπο “λύνεται” το πρόβλημα του κουρδίσματος των πληκτροφόρων κυρίως οργάνων, όπου οι εκτελεστές δεν μπορούν να παρέμβουν στο ακριβές τονικό ύψος των φθόγγων. Ένα άλλο πλεονέκτημα του ισοσυγκερασμένου κουρδίσματος είναι ότι οι κλίμακες είναι οι ίδιες σε κάθε τονικότητα κι έτσι μπορούν να γίνουν μεταφορές των συνθέσεων είτε προς τα πάνω είτε προς τα κάτω. Βασικό  μειονέκτημα  είναι η αντικατάσταση των λόγων μικρών ακεραίων από των άρρητο αριθμό , (κάτι που θα έκανε τους Πυθαγόρειους να φρίξουν). Αυτή η “προκρούστεια” παρέμβαση στα φυσικά διαστήματα (βλέπε παρακάτω Πίνακα 13), αλλοιώνει ελαφρώς  την αίσθηση του ακούσματος που ζητάει το ανθρώπινο αυτί.

 Ας δούμε τώρα πώς υπολογίζονται οι τιμές των ιδιοσυχνοτήτων των φθόγγων των 88 πλήκτρων του ισοσυγκερασμένου πιάνου. Δεχόμαστε ότι : (α) ο λόγος δύο διαδοχικών ιδιοσυχνοτήτων στο ισοσυγκερασμένο πιάνο ισούται με και (β) η ιδιοσυχνότητα αναφοράς είναι τα 440 Hz της Λα⁴.

Αν συμβολίσουμε με f_n όπου  τις ιδιοσυχνότητες των φθόγγων των 88 πλήκτρων του πιάνου (ξεκινώντας το μέτρημα των πλήκτρων από αριστερά), τότε στο Λα⁴ που βρίσκεται στη θέση 49 αντιστοιχεί ιδιοσυχνότητα f₄₉ = 440Ηz. Τότε με τις ιδιοσυχνότητες των φθόγγων των 39 πλήκτρων που βρίσκονται στα δεξιά του και με τις ιδιοσυχνότητες των φθόγγων των 48 πλήκτρων που βρίσκονται στα αριστερά του, σχηματίζει τους εξής λόγους:

Άρα

ή

Η σχέση (7) για υπολογίζει τις τιμές που παρατίθενται στον πίνακα 6:

ΠΙΝΑΚΑΣ 6

Αν θέλετε να συγκρίνετε το φυσικό με το ισοσυγκερασμένο κούρδισμα πιέστε εδώ για να ακούσετε  τη φυσική Λα μείζονα κλίμακα ακολουθούμενη από τρείς μεγάλες τρίτες και μια υπέρθεση από πέμπτες και κατόπιν πιέστε εδώ για να ακούσετε τα αντίστοιχα στη συγκερασμένη.

Το σύστημα των cents (Ellis 1885)

Είναι ένας εναλλακτικός τρόπος μέτρησης διαστημάτων που βασίζεται στους λογαρίθμους και είναι χρήσιμος για τη σύγκριση διαστημάτων διαφορετικών τονικών συστημάτων καθώς και για τη μέτρηση πολύ μικρών διαστημάτων. Αν σε κάθε ένα από τα 12 ίσα ημιτόνια της ισοσυγκερασμένης  κλίμακας  αποδώσουμε την τιμή των 100 cents  (c) τότε η οκτάβα ισοδυναμεί με 1200 cents.

Αν f₁, f₂ ,…,f₁₂ είναι οι 12 ίσες ιδιοσυχνότητες των 12 ημιτονίων της ισοσυγκερασμένης κλίμακας τότε :

Ο λόγος    αντιστοιχεί σε 100 cents

Ο λόγος αντιστοιχεί σε 200 cents

.
.
.
Ο λόγος αντιστοιχεί σε 1200 cents

Άρα αν οι ιδιοσυχνότητες f_n και f_k ορίζουν ένα τυχαίο διάστημα τότε :

Ο λόγος αντιστοιχεί σε c cents.

Με λογαρίθμιση της (8) (δεν έχει σημασία ως προς ποιά βάση), παίρνουμε:

  και τελικά

Η σχέση  (8) υπολογίζει την μια ιδιοσυχνότητα αν είναι γνωστή η άλλη και τα cents που αντιστοιχούν στο διάστημα που ορίζουν. Αντιστρόφως, αν είναι γνωστές οι ιδιοσυχνότητες τότε η σχέση (9) υπολογίζει τα cents που αντιστοιχούν στο διάστημα που ορίζουν. Αν θέλετε να υπολογίσετε διαστήματα σε cents πιέστε εδώ

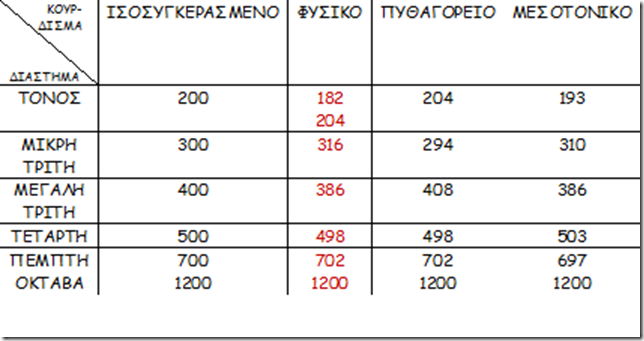
Στον πίνακα 7 συγκρίνονται τα διαστήματα στη φυσική (5η  – 6η στήλη) και στην ισοσυγκερασμένη (2η – 3η και 4η στήλη) κλίμακα ενώ η τελευταία στήλη περιέχει τις διαφορές. Είναι αξιοσημείωτο ότι οι τέταρτες και οι πέμπτες εμφανίζουν το μικρότερο “σφάλμα”.

ΠΙΝΑΚΑΣ 7

Name	Exact value in 12-TET	Decimal value in 12-TET	Cents	Just intonation interval	Cents in just intonation	Error
Unison (C)		1.000000	0	= 1.0000000	0.00	0
Minor second (C♯/D♭)		1.059463	100	≈ 1.06666…	111.73	−11.73
Major second (D)		1.122462	200	= 1.1250000	203.91	−3.91
Minor third (D♯/E♭)		1.189207	300	= 1.2000000	315.64	−15.64
Major third (E)		1.259921	400	= 1.2500000	386.31	+13.69
Perfect fourth (F)		1.334840	500	≈ 1.33333…	498.04	+1.96
Augmented fourth (F♯/G♭)		1.414214	600	= 1.4000000	582.51	+17.49
Perfect fifth (G)		1.498307	700	= 1.5000000	701.96	−1.96
Minor sixth (G♯/A♭)		1.587401	800	= 1.6000000	813.69	−13.69
Major sixth (A)		1.681793	900	≈ 1.66666…	884.36	+15.64
Minor seventh (A♯/B♭)		1.781797	1000	≈ 1.77777…	996.09	+3.91
Major seventh (B)		1.887749	1100	= 1.8750000	1088.27	+11.73
Octave (C)		2.000000	1200	= 2.0000000	1200.00	0

Να σημειώσουμε ότι στο σύστημα των cents το διάστημα που προκύπτει από την υπέρθεση δύο άλλων υπολογίζεται με άθροισμα και όχι με γινόμενο, Για παράδειγμα η πρόσθεση μια πέμπτης και μια τετάρτης δίνει
(3/2) ^. (4/3) = 2/1 (οκτάβα) ενώ στο σύστημα των cents 700+500 = 1200 (τα διαστήματα αυτά που η υπέρθεσή τους δημιουργεί οκτάβα ονομάζονται συμπληρωματικά)

Τέλος μια  μαθηματικής φύσης παρατήρηση:

(γ)

(δ)

Στο σχήμα (γ) φαίνονται οι ιδιοσυχνότητες 5 διαδοχικών φθόγγων που απέχουν μεταξύ τους διάστημα μιας οκτάβας σε γραμμική κλίμακα. Επειδή  η σχέση (7) που τις συνδέει είναι εκθετική οι αποστάσεις μεταξύ τους στη γραμμική κλίμακα είναι άνισες. Στο  σχήμα (δ) στο οποίο οι ίδιες ιδιοσυχνότητες παρουσιάζονται σε λογαριθμική κλίμακα, οι αποστάσεις ανάμεσά στις τιμές των ιδιοσυχνοτήτων είναι ίσες. Οι ίσες αυτές αποστάσεις των 1200 cents όμως στο σχήμα (δ) αντιστοιχούν σε διαφορετικές διαφορές Δf συχνοτήτων, οι οποίες είναι 110Hz, 220Hz, 440Hz και 880Hz αντίστοιχα. Στις ψηλές συχνότητες οι διαφορές αυτές είναι μεγαλύτερες. 

Διακροτήματα.

Στα παρακάτω σχήματα φαίνεται η χρονική εξέλιξη της παλινδρομικής κίνησης ενός σημείου στο οποίο συναντιούνται (συμβάλουν) δυο κύματα με παραπλήσιες συχνότητες.

Τα κίτρινα βέλη στο πάνω σχήμα, δείχνουν ότι κάποιες χρονικές στιγμές έχουμε αλληλοαναίρεση και τα πράσινα ότι κάποιες άλλες χρονικές στιγμές έχουμε ενίσχυση με αποτέλεσμα το πλάτος της ιδιόμορφης αυτής κίνησης να αυξομειώνεται περιοδικά, όπως δείχνει το μεσαίο και το κάτω σχήμα. Αν το κύματα που συμβάλουν είναι ηχητικά τότε επειδή η ένταση του ήχου είναι ανάλογη του τετραγώνου του πλάτους, το αυτί  μας αντιλαμβάνεται αυτές τις περιοδικές διακυμάνσεις του πλάτους ως περιοδικές μεταβολές της έντασης του ήχου. Αυτές οι περιοδικές μεταβολές της έντασης του ήχου ονομάζονταιδιακροτήματα.

Γενικά είναι δύσκολο να προσδιοριστεί πόσο μικρές είναι οι διαφορές στη συχνότητα που μπορεί να αντιληφθεί το ανθρώπινο αυτί. Εκτός από το ότι αυτό εξαρτάται από την μουσική εκπαίδευση του ακροατή, καθορίζεται και από διάφορους άλλους παράγοντες όπως είναι η τιμή της συχνότητας, η ένταση και η διάρκεια του ήχου, το πόσο απότομη είναι η μεταβολή της συχνότητας, το πόσο σύνθετος (πλούσιος σε αρμονικούς) είναι ο ήχος και φυσικά από τον τρόπο μέτρησης. Αν ακούσουμε ξεχωριστά δύο νότες που οι συχνότητές τους διαφέρουν ελάχιστα  πολύ δύσκολα θα καταλάβουμε τη διαφορά. Ενώ αν συνηχήσουν θα αντιληφθούμε το διακρότημα.Εδώ  ακούγεται το διακρότημα που δημιουργεί η συνήχηση της Λα³ στα 220 Hz με την ίδια νότα αυξημένη κατά 2Hz.

Στον Πίνακα 5 είδαμε ότι οι διαφορές των συχνοτήτων των φθόγγων Μι⁴ και Λα⁴  ανάμεσα στη φυσική κλίμακα της Ντο ματζόρε και της Ρε ματζόρε είναι 4,2 Hz = 21,9 cents και 5,5 Hz = 21,5 cents  αντίστοιχα. Πόσο αισθητές είναι άραγε οι διαφορές αυτές; Σύμφωνα με μια υπεραπλουστευμένη άποψη η ελάχιστα αξιοσημείωτη διαφορά (Just-noticeable difference) στην τονικότητα είναι περίπου 5 cents, οπότε οι διαφορές των 21,9 και 21,5 cents, γίνονται σίγουρα αντιληπτές από κάποιο εξασκημένο αυτί, ενώ κάποια άλλα αυτιά –όπως το δικό μου- ίσως να μην τις εντοπίσουν, μια που αυτό είναι εντελώς υποκειμενικό.

Πολύ χαρακτηριστική , είναι η άποψη  του Ελισαίου Γιανίδη (από την πραγματεία του «Η Βυζαντινή μουσική και η εναρμόνισή της«, Εκδόσεις «Γκοβόστη«) ο οποίος –  αναφερόμενος στη φωνητική μουσική- συγκρίνει την ποιότητα των ακουσμάτων των ισοσυγκερασμένων  και φυσικών διαστημάτων:

“…Τώρα τι γίνεται με τη συγκερασμένη; Αυτή, καθώς καταλάβαμε, έχει ελαφρές παραφωνίες. Η μεγάλη τρίτη π.χ. ντο-μι, είναι μεγαλύτερη απ’ τη φυσική. Ο φθόγγος ο μεταξύ ντο και ρε, όταν τον χρησιμοποιούμε ως ντο δίεση είναι πολύ υψηλός, όταν ως ρε ύφεση πολύ χαμηλός. Πως κατορθώνουμε με αυτό το υλικό να κάνουμε μουσική; Η απάντηση είναι η ακόλουθη: Ότι η ακοή μας έχει ένα περιθώριο ανοχής και τα λάθη αυτά, που είναι εν γένει ανεπαίσθητα  βρίσκονται συνήθως μέσα σ’ αυτό το περιθώριο, και επομένως περνούν απαρατήρητα, δηλαδή ο ακροατής παίρνει τους φθόγγους για φυσικούς…

…Το ιδανικό διάστημα για το σημερινό άνθρωπο είναι πάντα φυσικό. Το (συγκερασμένο) το δέχεται, να πούμε, σαν αντιπρόσωπο του φυσικού. Γίνεται ακουστική απάτη. (Εκείνος που κουρδίζει το πιάνο ακολουθώντας τις πέμπτες λα-μι-σι … είναι υποχρεωμένος να τις κάμει λίγο λειψές (βλ. παρακάτω Πίνακα 13), γιατί αλλιώς η συγκερασμένη κλίμακα δεν μπορεί να συμπληρωθεί. Ε, λοιπόν, σ’ αυτή τη νόθεψη των διαστημάτων οδηγιέται απ’ τη μεγάλη πείρα, η φύση δεν τον οδηγεί. Γι’ αυτό ένας που έμαθε να κουρδίζει μονάχα το βιολί δε θα πετύχει στο κούρδισμα του πιάνου. Συνήθισε στην αλήθεια και δεν πετυχαίνει στο ψέμμα. Όμοια, τη φυσική μεγάλη τρίτη ντο-μι κάθε μουσικός τη βρίσκει με βεβαιότητα. Αν όμως ζητήσετε να σας δώσει τη συγκερασμένη μεγάλη τρίτη, όχι μονάχα ο βιολιστής δεν θα μπορέσει να την εύρει παρά ούτε και ο κουρδιστής του πιάνου, γιατί δεν απόχτησε την πείρα γι’ αυτό το διάστημα, δεν έμαθε να εκτιμά το λάθος της τρίτης. Θα την εύρει με μια σειρά από πέμπτες: ντο-σολ-ρε-λα-μι (βλ. παρακάτω το Μεσοτονικό κούρδισμα)  Το συμπέρασμα μου είναι πως το αφτί του σημερινού ανθρώπου τον οδηγεί μονάχα στα φυσικά διαστήματα. Για τ’ άλλα χρειάζεται κάποια προσπάθεια και ιδιαίτερα τεχνάσματα…).

(Αν θέλετε να κάνετε τεστ για την ικανότητά σας να αντιλαμβάνεστε τις διαφορές στα τονικά ύψη πιέστε εδώ.)

H κλίμακα του Πυθαγόρα.

Είναι μια κλίμακα που δημιουργεί το φθογγικό της υλικό (σε εύρος μεγαλύτερο της οκτάβας) με υπέρθεση καθαρών πέμπτων (λόγος συχνοτήτων 3/2), ξεκινώντας από μια συγκεκριμένη  ιδιοσυχνότητα f. Οι συχνότητες των υπόλοιπων φθόγγων υπολογίζονται είτε πολλαπλασιάζοντας  την f με (3/2)ⁿ ανεβαίνοντας είτε με (2/3)ⁿ κατεβαίνοντας όπου n = 0,1,2,…. Έτσι από την υπέρθεση 12 πέμπτων, με πολλαπλασιασμό ή διαίρεση του κάθε αποτελέσματος με την κατάλληλη δύναμη του 2  για να φέρουμε τις συχνότητες στην ίδια οκτάβα  (f_n = 2ⁿ f ,  n = 1,2,3,.. είναι η σχέση που συνδέει δύο συχνότητες σε απόσταση n οκτάβων) δημιουργούνται οι φθόγγοι μιας χρωματικής κλίμακας.

ΠΙΝΑΚΑΣ 8

Η επιλογή επτά κατάλληλων φθόγγων που προκύπτουν από την υπέρθεση έξι συνεχόμενων πέμπτων από την παραπάνω ακολουθία (κόκκινο πλαίσιο) και η τοποθέτησή τους κατά αύξουσα σειρά,  δίνει μια διατονική επτάφθογγη κλίμακα στην τονικότητα της f:

ΠΙΝΑΚΑΣ 9

Συγκρίνοντας τον πίνακα 2 με τον πίνακα 9 παρατηρούμε ότι η πυθαγόρεια διατονική κλίμακα δίνει διαφορετικές μεγάλες τρίτες, μεγάλες έκτες και μεγάλες έβδομες από τη φυσική και διαφορετικά ημιτόνια (εκτός από το 256/243 το οποίο λέγεται διατονικό δημιουργεί και ένα χρωματικό με λόγο 2187/2048). Επίσης εμφανίζεται ένας μόνο τόνος (9/8) και διάφωνα διαστήματα μια που αρκετοί από τους λόγους που δημιουργούνται περιέχουν μεγάλους ακεραίους.

Τα τρία καθαρά διαστήματα, δηλαδή η οκτάβα (2/1) η πέμπτη (3/2) και η τέταρτη (4/3), παράγονται από τους αριθμούς 1,2,3,4 και συνδέονται με τη σχέση 2/1 = (3/2) ^. (4/3). Η τετράδα αυτή είχε ιδιαίτερη σημασία για τη μουσική θεωρία των Πυθαγορείων, την οποία ονόμαζαν “τετρακτύ”. Οι τέσσερεις αυτοί αριθμοί δίνουν άθροισμα το 10 που το θεωρούσαν τον πληρέστερο αριθμό.

Ήξεραν οι Πυθαγόρειοι Φυσική;

Ας ξεκινήσουμε με δυο διαπιστώσεις. Οι Πυθαγόρειοι γνώριζαν ότι οι ήχοι που μπορούν να παράγουν μια οργανωμένη μουσική δομή εκφράζονται με λόγους ακεραίων και μάλιστα όσο πιο ευχάριστα ακούγονται οι ήχοι τόσο ποιό απλοί είναι οι λόγοι που τους εκφράζουν. Όπως είδαμε πιο πάνω οι λόγοι αυτοί προκύπτουν από την αρμονική σειρά μιας θεμελιώδους ιδιοσυχνότητας. Γνώριζαν επίσης ότι το τονικό ύψος των φθόγγων σχετίζεται με το μήκος των χορδών και των ηχητικών σωλήνων. Επειδή όμως θα ήταν άστοχο να μιλήσουμε για Φυσική επιστήμη πριν από το Γαλιλαίο και το Νεύτωνα θα επαναδιατυπώσουμε το αρχικό μας ερώτημα :

Είναι  δυνατόν όλη η κοσμοθεωρία των Πυθαγορείων που ξεκινάει από την ανθρώπινη κλίμακα και επεκτείνεται στα ουράνια σώματα με την “αρμονία των  σφαιρών” και η οποία – χρησιμοποιώντας ως εργαλείο μελέτης τη μουσική – δομείται με βάση τα μαθηματικά, να στηρίζεται σε a priori παραδοχές που δημιουργεί μια παραγωγική νοητική διαδικασία ή μήπως πρόκειται για μια κατά βάση εμπειρική φιλοσοφία που προχωράει επαγωγικά;

Αν ψάξουμε την απάντηση σε ιστορικές πηγές θα απογοητευτούμε γιατί είναι ελάχιστες. Ο Πυθαγόρας δεν άφησε γραπτά κι έτσι  όσες πληροφορίες σχετικά με αυτόν και το έργο του διασώζονται προέρχονται από έμμεσες πηγές και θα πρέπει να είμαστε πολύ επιφυλακτικοί για την αξιοπιστία τους. Αυτός είναι και ο λόγος που, σε συνδυασμό με τη σύγχυση που δημιουργεί η έκταση του κινήματος των Πυθαγορείων μέσα στο χρόνο, κάνει τις απόψεις των μελετητών για την μεθοδολογία τους εκ διαμέτρου αντίθετες. Τα επιχειρήματα και των δυο πλευρών είναι πολλά. Όμως όταν υπάρχουν τέτοιες αντιθέσεις, η αλήθεια πρέπει να βρίσκεται κάπου στην μέση. Τη θέση αυτή υποστηρίζει  ο Παύλος Καϊμάκης στο εξαιρετικό βιβλίο του«Φιλοσοφία και μουσική» και μας βρίσκει απολύτως σύμφωνους. Θεωρώ πως ο χαρακτηρισμός της ανακάλυψης από τους Πυθαγορείους της σχέσης των λόγων των συχνοτήτων με τα μήκη των χορδών, ως “μια από τις ισχυρότερες ωθήσεις της ανθρώπινης επιστήμης γενικά” από έναν από τους μεγαλύτερους φυσικούς του 20ού αιώνα τον νομπελίστα  Werner Heisenberg  τα λέει όλα!

Το Μεσοτονικό κούρδισμα (Quarter – comma meantone tunning)

Είναι ένα κούρδισμα που παράγει το φθογγικό του υλικό (σε εύρος μεγαλύτερο της οκτάβας) χρησιμοποιώντας την Πυθαγόρεια λογική υπέρθεσης πέμπτων, εξαλείφοντας τη διαφορά των δύο τόνων του φυσικού κουρδίσματος (διάστημα 81/80=σύντονο κόμμα)  και – σε μια από τις εκδοχές του – δημιουργεί  φυσικές μεγάλες τρίτες.

Στον παρακάτω πίνακα συγκρίνονται οι μεγάλες τρίτες του φυσικού και του Πυθαγόρειου κουρδίσματος.

  ΠΙΝΑΚΑΣ 10

Στο φυσικό κούρδισμα η μεγάλη τρίτη ισούται με την υπέρθεση δυο διαφορετικών τόνων : 5/4 = (9/8) ^. (10/9) , ενώ στο Πυθαγόρειο ισούται με την υπέρθεση δυο ίσων τόνων : 81/64 = (9/8) ^. (9/8) και δεν είναι φυσική. Το Μεσοτονικό κούρδισμα που θα περιγράψουμε, είναι η μεσοβέζικη λύση που δημιουργεί καθαρές φυσικές τρίτες που περιέχουν δυο ίσους τόνους με το τίμημα της “πειραγμένης” πέμπτης. Για να δούμε πως γίνεται αυτό θα ξεκινήσουμε από την βασική παραδοχή που είναι η δημιουργία φυσικών τρίτων με υπέρθεση πέμπτων.

Ξεκινώντας από το Ντο, με επαλληλία τεσσάρων φυσικών πέμπτων παίρνουμε την ακολουθία :

Ντο – Σολ – Ρε – Λα – Μι

Το διάστημα που δημιουργείται ανάμεσα στο Ντο και το Μι έχει λόγο: (3/2)⁴ = 81/16.

Στον ίδιο φθόγγο μπορούμε να φτάσουμε και με την εξής επαλληλία φυσικών διαστημάτων:

Ντο – Ντο – Σολ – Ντο – Μι

Η διαδοχική υπέρθεση μιας οκτάβας 2/1 (Ντο – Ντο) μιας καθαρής πέμπτης 3/2 (Ντο – Σολ) μιας καθαρής τετάρτης 4/3  (Σολ – Ντο) και μιας μεγάλης τρίτης 5/4 (Ντο – Μι)  δημιουργούν ανάμεσα στο Ντο και το Μι διάστημα με λόγο:

(2/1) ^. (3/2) ^. (4/3) ^. (5/4) = 120/24 = 5/1. 

Το παραπάνω διάστημα Ντο – Μι δημιουργεί φυσική καθαρή τρίτη, αν φέρουμε το Μι μέσα στην οκτάβα Ντο – Ντο διαιρώντας το με 2² : 5/1 : 2² = 5/4

Το διάστημα Ντο – Μιείναι μικρότερο από το Ντο – Μι κατά (81/16) : (5/1) = (81/16) : (80/16) = 81/80 = 21,506 cents  (που όπως αναφέραμε πιο πάνω είναι η διαφορά ανάμεσα στον μικρό και μεγάλο τόνο της φυσικής κλίμακας και ονομάζεται σύντονο ή διδυμικό κόμμα). Άρα για να πάρουμε φυσική τρίτη θα πρέπει να αμβλύνουμε την φυσική πέμπτη. Έστω χ η τιμή της, τότε θα πρέπει :

χ⁴ = 5/1 ή χ = 5^1/4

Έτσι υπολογίσαμε την τιμή της  “πειραγμένης” πέμπτης του μεσοτονικού κουρδίσματος, η οποία είναι βέβαια όπως και το 2^1/12 άρρητος αριθμός, και αντιστοιχεί σε 696,578 cents, δηλαδή είναι κατά 5,377cents μικρότερη σε σχέση με τα 701,955 cents της φυσικής πέμπτης. Τα 5,377 cents είναι το 1/4 του σύντονου κόμματος (εξ ου και η ονομασία Quarter – comma  tunning). 

Για να δημιουργήσουμε το φθογγικό υλικό, όπως και στο πυθαγόρειο κούρδισμα, ξεκινάμε από μια συχνότητα f, και υπερθέτουμε  12 “πειραγμένες” πέμπτες. Πολλαπλασιάζουμε ή διαιρούμε κάθε αποτέλεσμα με την κατάλληλη δύναμη του 2  για να φέρουμε τις συχνότητες στην ίδια οκτάβα. Έτσι προκύπτουν οι φθόγγοι μιας χρωματικής κλίμακας.

ΠΙΝΑΚΑΣ 11

Η επιλογή επτά κατάλληλων φθόγγων που προκύπτουν από την υπέρθεση έξι συνεχόμενων πέμπτων από την παραπάνω ακολουθία (κόκκινο πλαίσιο) και η τοποθέτησή τους με αύξουσα σειρά,  δίνει μια διατονική επτάφθογγη κλίμακα στην τονικότητα της f:

ΠΙΝΑΚΑΣ 12

Ο τόνος 5^1/2/2 που δημιουργεί το συγκεκριμένο κούρδισμα ισοδυναμεί με 193,104 cents και βρίσκεται περίπου μισό κόμμα (= 10,753 cents) κάτω από τον μεγάλο τόνο (9/8) της φυσικής κλίμακας που αντιστοιχεί σε 203,91 cents και άλλο τόσο περίπου πάνω από τον μικρό τόνο (10/9) της φυσικής κλίμακας που αντιστοιχεί σε 182,23 cents. Έτσι ενώ στο διάστημα της μεγάλης τρίτης Ντο – Μι στο φυσικό κούρδισμα το το Ρε απέχει έναν μεγάλο τόνο (9/8) από το Ντο και έναν μικρό (10/9) από το Μι (πίνακας 3) , στο αντίστοιχο διάστημα στο μεσοτονικό [f έως (5/4)f στον Πίνακα 12] το Ρε [(5^1/2/2) f] βρίσκεται ακριβώς στην μέση (πίνακας 12). Έτσι δικαιολογείται και η ονομασία του κουρδίσματος “μεσοτονικό”.

Ο απολογισμός σε …cents

ΠΙΝΑΚΑΣ 13

Στον Πίνακα 13 γίνεται η σύγκριση μερικών χαρακτηριστικών διαστημάτων σε cents στα τέσσερα κουρδίσματα που περιγράψαμε. Παρατηρούμε ότι η πέμπτη και η τέταρτη παρουσιάζουν σε σχέση με το φυσικό κούρδισμα διαφορές μικρότερες ή ίσες με 5 cents (την ελάχιστη αξιοσημείωτη διαφορά JND) ενώ τις μεγαλύτερες αποκλίσεις παρουσιάζουν η μεγάλη και η μικρή τρίτη στο Πυθαγόρειο και στο ισοσυγκερασμένο κούρδισμα σε σχέση με το φυσικό.

Κάθε κούρδισμα λοιπόν λύνει κάποια προβλήματα, δημιουργώντας άλλα.Το πρόβλημα γενικά είναι άλυτο. Γι αυτό όλα τα κατά καιρούς κουρδίσματα είναι συμβιβαστικές λύσεις, όλα µε διαφορετικά προτερήματα και μειονεκτήματα που έχουν να κάνουν µε το φθογγικό υλικό που χρησιμοποιείται περισσότερο ανά εποχή και τις μουσικές αναγκαιότητες της κάθε εποχής. Το Μεσοτονικό  κούρδισμα χρησιμοποιήθηκε κατά τον 16ο και 17ο αιώνα, ενώ το 12 τόνων ισοσυγκερασμένο κούρδισμα επικράτησε από τον 19ο αιώνα και μετά. 

Τα χαμένα και κερδισμένα … cents στο Πυθαγόρειο και στο Μεσοτονικό κούρδισμα και ο Κύκλος όπου οι 12 πέμπτες συναντούν τις 7 οκτάβες ή Κύκλος των Πέμπτων.

Αν στον Πίνακα 8 της Πυθαγόρειας κλίμακας, κάνουμε αναγωγή σε απόλυτα τονικά ύψη, αντικαθιστώντας π.χ στην ιδιοσυχνότητα f την τιμή που αντιστοιχεί στη νότα Ρε, παίρνουμε την αλληλουχία των φθόγγων  του παρακάτω πίνακα 14:

ΠΙΝΑΚΑΣ 14

ΛΑ♭

ΜΙ♭

ΣΙ♭

ΦΑ

ΝΤΟ

ΣΟΛ

ΡΕ

ΛΑ

ΜΙ

ΣΙ

ΦΑ#

ΝΤΟ#

ΣΟΛ#

Η χρωματική κλίμακα που δημιουργεί η υπέρθεση δώδεκα  πέμπτων έχει ένα “μικρό” μειονέκτημα μαθηματικής φύσης: κάθε πέμπτη περιέχει 7 ημιτόνια, ενώ κάθε οκτάβα περιέχει 12 ημιτόνια. Η υπέρθεση των 12 πέμπτων δίνει μια συχνότητα (3/2)¹² f = 129,74f, ενώ οι 7 οκτάβες αντιστοιχούν σε συχνότητα 2⁷ f = 128 f. Η διαφορά αυτή (λόγος 1,0136), που αντιστοιχεί σε περίπου 23,4 cents (περίπου το 1/4 του ημιτονίου) είναι το λεγόμενο Πυθαγόρειο κόμμα. Αυτό έχει ως αποτέλεσμα τη μη ταύτιση της ΛΑ♭με τη Σολ #. Ένας τρόπος “αντιμετώπισης” του προβλήματος είναι η “προκρούστεια” περικοπή της δωδέκατης πέμπτης κατά 23,4 cents. Έτσι  από τα 702 περίπου cents που αντιστοιχούν στην καθαρή πέμπτη απομένουν περίπου 678,6 cents και δημιουργείται έτσι ένα διάστημα (wolf interval) που παρομοιάζεται ότι ηχεί σαν την κραυγή του λύκου. Στο Μεσοτονικό κούρδισμα που οι “πειραγμένες” πέμπτες είναι μικρότερες από τις φυσικές το χάσμα είναι ακόμα μεγαλύτερο και και έτσι για να δώσουν οι 12 πέμπτες τις 7 οκτάβες θα πρέπει η δωδέκατη να επιμηκυνθεί στα 737,6 cents. Στο ισοσυκγερασμένο  όμως κούρδισμα των 12 τόνων όπου η πέμπτη ισοδυναμεί με 700 cents , οι 12 πέμπτες δίνουν ακριβώς 12 ^. 700 = 8400 cents, όσα ακριβώς δίνουν και οι 7 οκτάβες : 7 ^. 1200 = 8400 cents. Έτσι δημιουργείται ένας κύκλος όπου η υπέρθεση 12 πέμπτων δίνει τους 12 τόνους της χρωματικής κλίμακας. Ο κύκλος αυτός λέμε ότι ‘κλείνει”. Δηλαδή ανεβαίνοντας κατά 12 πέμπτες  ξεκινώντας από έναν τυχαίο τόνο καταλήγουμε στον τόνο απ’ όπου ξεκινήσαμε.

Η χρησιμότητα και η σημασία του κύκλου των πέμπτων για τους μουσικούς ξεφεύγει από τα πλαίσια αυτής της ανάλυσης. Κλείνοντας εδώ αξίζει να σημειώσουμε ότι εξαιτίας της συμπληρωματικότητας των διαστημάτων της πέμπτης και της τέταρτης, ο κύκλος όταν διαγράφεται κατά τη φορά την δεικτών του ρολογιού δίνει αύξουσες πέμπτες ή φθίνουσες τέταρτες. Τέλος η επικάλυψη στο κάτω μέρος του κύκλου των ζευγαριών υφέσεων και των διέσεων δείχνει την εναρμόνια ισοδυναμία ανάμεσά τους.

Και πάλι η φυσική διατονική κλίμακα : 5-limit tuning . Ένα μαθηματικό “παιχνίδι” με τους πρώτους αριθμούς.

Η διατονική κλίμακα μπορεί να παραχθεί και με τη χρήση των πρώτων αριθμών (1, 2, 3, 5) έως το 5 (5-limit tuning). Οι αριθμοί αυτοί με τους κατάλληλους συνδυασμούς δυνάμεών τους δίνουν μια μικρή τρίτη 2^{1 .} 3^{1  .} 5^–1 = 6/5, μια μεγάλη τρίτη 5^{1 .} 2 ^–2 = 5/4 και μια καθαρή πέμπτη
3^{1 .} 2 ^–1 = 3/2.

Η δημιουργία μιας μείζονος κλίμακας  πχ. του Ντο γίνεται με τη χρήση των προηγούμενων διαστημάτων και με την απαίτηση οι συγχορδίες ΝΤΟ^ο -ΜΙ-ΣΟΛ,   ΦΑ-ΛΑ-ΝΤΟ¹ και ΣΟΛ-ΣΙ-ΡΕ, να είναι μείζονες δηλαδή να περιέχουν μια μεγάλη τρίτη πρώτα και μετά μια μικρή (λόγοι 4:5:6). Η υπέρθεση της μικρής και μεγάλης τρίτης δίνει μια καθαρή πέμπτη, αφού (5/4) ^. (6/5) = 3/2 . Η διαδικασία έχει ως εξής:
Αν αποδώσουμε στο ΝΤΟ⁰ την τιμή της ιδιοσυχνότητας f, τότε η μείζονα συγχορδία ΝΤΟ^ο -ΜΙ-ΣΟΛ δίνει για την ιδιοσυχνότητα του ΜΙ την τιμή (5/4)f και για την ιδιοσυχνότητα του ΣΟΛ την  τιμή (5/4)f ^. (6/5) = (3/2)f.
Η μείζονα συγχορδία ΦΑ – ΛΑ- ΝΤΟ¹ δίνει ξεκινώντας από το ΝΤΟ¹ που βρίσκεται μια οκτάβα πάνω από το ΝΤΟ^ο  -oπότε έχει ιδιοσυχνότητα 2f- για την ιδισυχνότητα του ΛΑ την τιμή 2f:(6/5) = (5/3)f και για την ιδιοσυχνότητα του ΦΑ την τιμή (5/3)f: (5/4) = (4/3)f.
Τέλος η μείζονα συγχορδία ΣΟΛ-ΣΙ-ΡΕ , ξεκινώντας από το ΣΟΛ δίνει για την ιδιοσυχνότητα του ΣΙ την τιμή (3/2)f ^. (5/4) = (15/8)f και για την ιδιοσυχνότητα του ΡΕ την τιμή (15/8)f ^. (6/5) = (18/8)f>2f , οπότε για να την φέρουμε εντός οκτάβας διαιρούμε με το 2 και παίρνουμε (9/8)f.
Τοποθετώντας τις ιδιοσυχνότητες που βρήκαμε κατά αύξουσα σειρά έχουμε:

f              (9/8)f      (5/4)f     (4/3)f    (3/2)f    (5/3)f      (15/8)f     2f

ΝΤΟ^Ο           ΡΕ               ΜΙ          ΦΑ            ΣΟΛ      ΛΑ           ΣΙ        ΝΤΟ¹

που είναι η μείζονα φυσική κλίμακα του Ντο.

Κατακλείδα : Η διατονική κλίμακα του Πτολεμαίου.

Πρόκειται για τη γνωστή φυσική διατονική μείζονα κλίμακα η οποία παράγεται από δυο όμοια τετράχορδα. Τα τετράχορδα σύμφωνα με την αρχαία Ελληνική θεωρία της μουσικής είναι κατιούσες καθαρές τέταρτες με δομή Τόνος – τόνος – ημιτόνιο. Τα τετράχορδα που χρησιμοποίησε ο Πτολεμαίος αποτελούνταν από έναν μεγάλο τόνο με λόγο συχνοτήτων 9/8, έναν μικρό με λόγο συχνοτήτων 10/9 και ένα ημιτόνιο με λόγο συχνοτήτων 16/15.

Αν θέλετε να ακούσετε μουσική γραμμένη με βάση τις αρχαίες ελληνικές κλίμακες πιέστε: Δημήτρης Τερζάκης

Και μια ερώτηση: Το καλοκαίρι σε ένα κονσέρτο πως επηρεάζουν οι υψηλές θερμοκρασίες τα έγχορδα όργανα;

Απάντηση: Η ζέστη προκαλεί διαστολή στις χορδές με αποτέλεσμα να μειώνεται η δύναμη που τις τεντώνει, οπότε σύμφωνα με τη σχέση (5) μειώνεται η συχνότητα και ο ήχος ακούγεται πιο βαρύς. Τι συμβαίνει άραγε με τα πνευστά; Για την απάντηση ανατρέξτε στο Β’ μέρος: Οι ηχητικοί σωλήνες. 

ΑΝΑΦΟΡΕΣ:

Βιβλιογραφία:

1. Haliday – Resnick : Φυσική Μέρος Α
2. Serway : Physics for scientists & engineers τόμος ΙΙΙ
3. P.G. Hewit : Οι έννοιες της Φυσικής τόμος Ι
4. Π. Καϊμάκης : Φιλοσοφία και Μουσική
5. U. Michels : Άτλας της μουσικής τόμος Ι

Internet.

1. Just intonation
2. HyperPhysics
3. Ptolemy’s intense diatonic scale
4. Cent
5. Meantone temperament
6. Musical system of ancient Greece
7. Tetrachord
8. Pythagorean tuning
9. Circle of fifths
10. Enharmonic
11. Chromatic circle
12. Pitch class
13. Syntonic temperament
14. Regular temperament
15. Five-limit tuning
16. Quarter-comma meantone
17. Equal temperament
18. Scientific pitch notation
19. A440 (pitch standard)
20. Pitch